参考:
1. 红黑树简介
1.1 为什么要使用红黑树
红黑树是一种自平衡的二叉查找树。
对于二叉查找树,容易出现严重单边长的情况,会导致查询效率降低,于是出现了平衡二叉查找树,包含 AVL 树, AVL 树通过旋转达到平衡,平衡因子为 1,过于严格,插入时会导致大量旋转,性能降低,于是出现了红黑树。
红黑树使用两种颜色来达到维持平衡的目的!
1.2 红黑树特性
红黑树有 5 个知名特性
- 每个节点或者是黑色,或者是红色。
- 根节点是黑色。
- 每个叶子节点(NULL)是黑色。 注意:这里叶子节点,是指为空(NULL)的叶子节点!
- 如果一个节点是红色的,则它的子节点必须是黑色的。 注意:可以出现父节点和子节点都是黑色
- 任意一个节点到其叶子节点的所有路径上包含相同数目的黑节点。
红黑树的最坏情况:最长路径是最短路径的 2 倍。

1.3 平衡手段
对于红黑树的平衡,有两种方法:
- 通过旋转,也就是和AVL的旋转一样,左旋和右旋。旋转也是改变颜色的一种方案,主要是达到颜色平衡的目的。
- 通过改变节点的颜色,也就是对节点重新着色。
2. 插入节点
2.1 插入的是根节点
直接涂黑即可。
2.2 插入节点的父节点是黑色
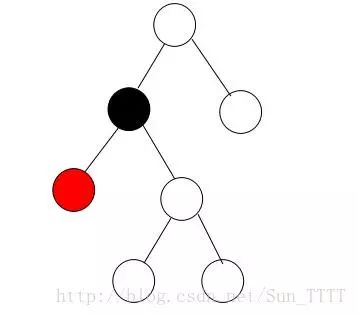
这个时候插入一个红色的节点并没有对这五个性质产生破坏。所以直接插入不用在进行调整操作。
2.3 插入节点父节点是红色
2.3.1 父红叔红
要插入节点的父节点是红色的,叔叔节点也是红色的,这时候通过变色达到平衡。

将父节点和叔叔节点变为黑色,祖父节点变为红色(祖父节点之前肯定为黑色),就可以让此子树达到红黑平衡。路径上黑色节点数量不变。
然后以祖父节点为根据,继续调整。
2.3.2 父红叔黑,插入节点和父节点在同一边
同一边是相当于祖父而言,若父亲位于祖父的左边,插入节点也为祖父的左边,则为同一边。
下图仅展示局部
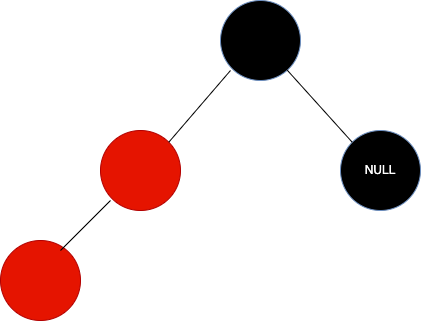
此时,通过旋转即可解决,如上,对祖父节点进行一次右旋,同时将父节点和祖父节点颜色互换,就变成了

达到了平衡。
为什么会想到这么做?
上面我们提到解决这个问题的本质就是变色,旋转也是为了更好的变色,变色肯定变的是插入节点的父节点,若父节点变为黑色,则此路径多了一个黑色节点,叔叔也需要多一个黑色结点,但叔叔本来就是黑色的,怎么才能多一个黑色节点呢?
那么我们就可以通过旋转,使父节点路径少一个节点。此时叔叔路径多个一个黑色的祖父节点,变黑即可,即为上述方式。
2.3.3 父红叔黑,插入节点和父节点非同一边
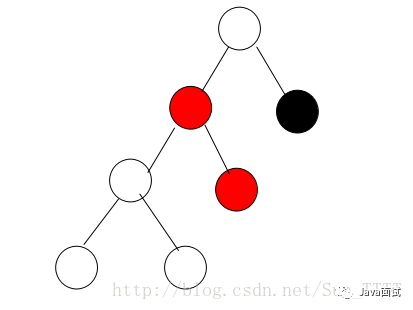
先对父节点进行左旋,使之变为同一边的 case,然后按同一边方案处理即可,左旋后如下:

3. 删除
4. 其它
4.1 插入节点的颜色
为保持平衡,插入节点的颜色初始化为红色,才有可能不破坏平衡。
4.2 变色时,为什么也需要改变祖父节点颜色?
只改变父节点和叔叔节点的颜色不行吗?
如下的左图是红黑树的一个局部,一开始是满足红黑树的特性的,在其中插入了红色节点10,两个红节点连在一起了,不再满足红黑树的特性 4。
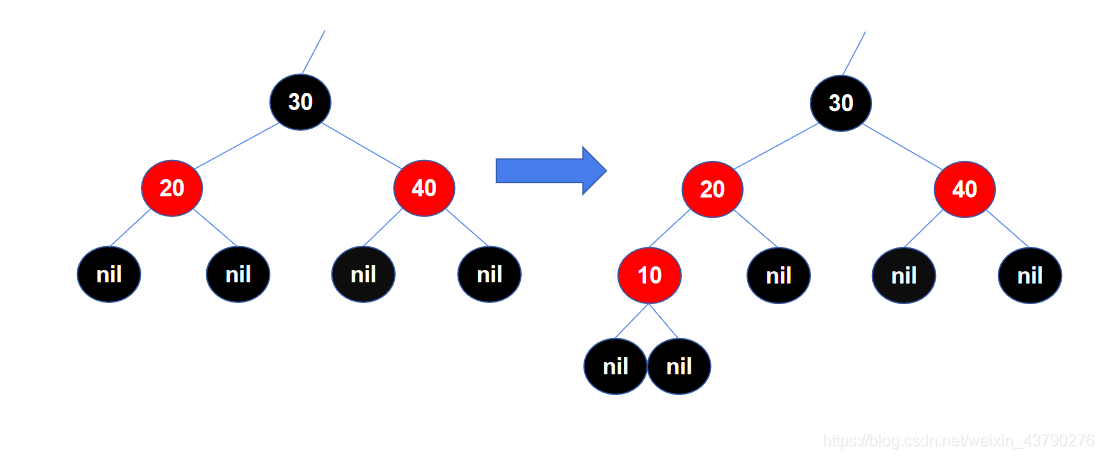
由于父节点和叔叔节点都为红色,需要变色。
通过变色,先将节点 20 变成黑色,特性 4 满足了,但又不满足特性 5,所以继续将节点 30 变成红色,节点 40 变成黑色。
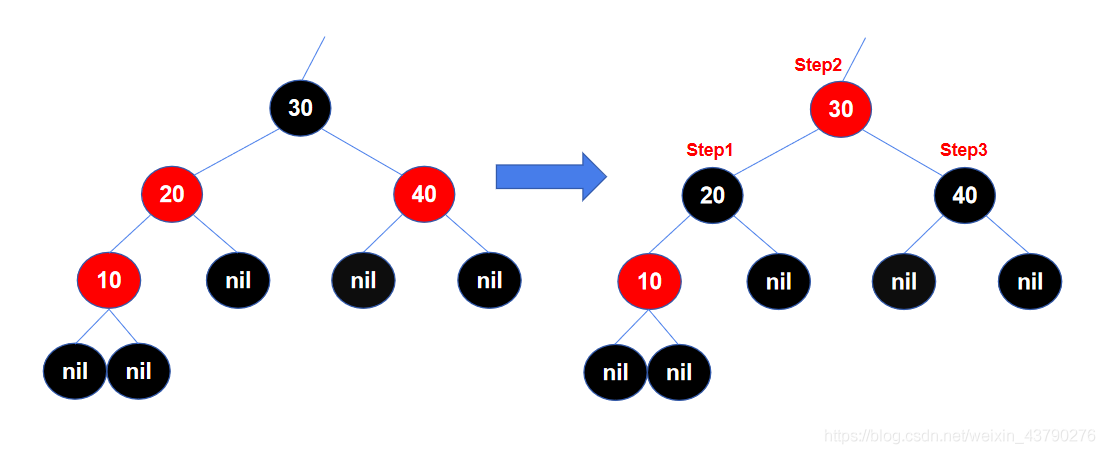
若我们不改变 30 为红色,则对于 30 的父节点来说,这个子树上多了一个黑色节点,破坏了平衡。
经过3次变色后,从局部看,已经重新满足了红黑树的特性。但是,从整棵树来看,还不一定满足红黑树的特性,如果节点 30 的父节点也是红色,则还需要继续对这棵树进行调整。
