参考：AVL 树

1. 什么是 AVL 树

AVL 树，自平衡二叉查找树，名字来源于作者首字母大写。

在 AVL 树中，任一节点对应的两颗子树最大高度差为1，因此，AVL 树也称为高度平衡树。查找、删除、插入平均、最坏复杂度都是O(log n)，增加和删除元素的操作可能触发一次或多次树旋转。

2. 平衡因子

AVL 树使用节点中的高度（height）属性测量节点是否平衡。高度是节点到最远叶子节点的距离。

指定节点 children 的相对高度决定该节点是否平衡，左右子树高度相差最大为1，高度差被称为平衡因子。

下面是一颗 AVL 树：

蓝色表示高度，绿色表示平衡因子。

插入40后如下所示：

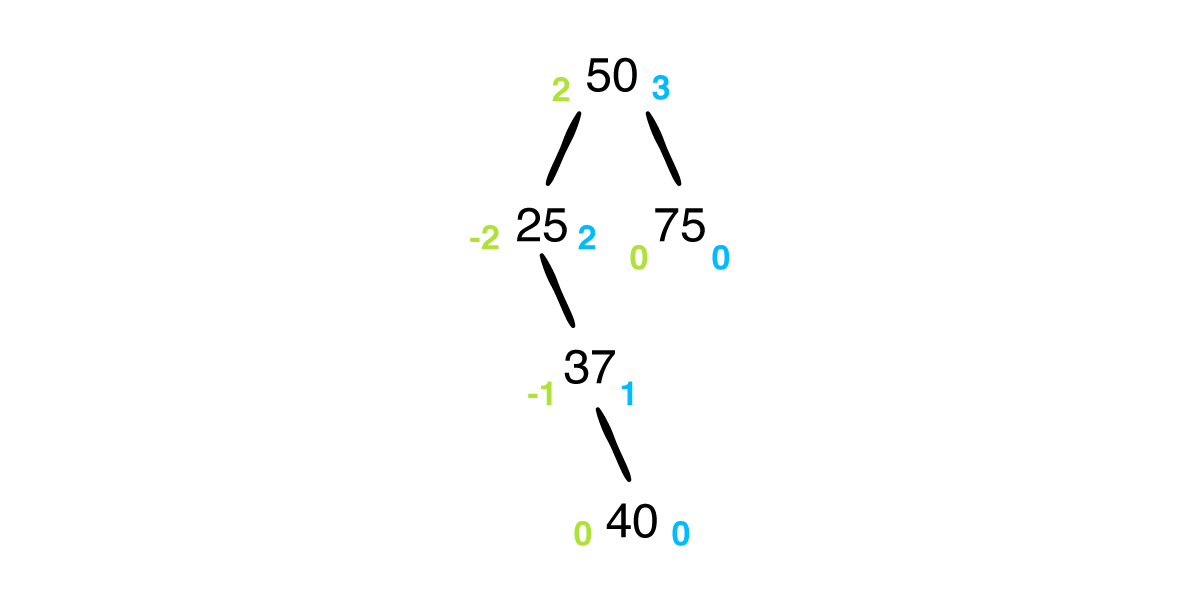
插入40后，平衡因子出现了大于等于2，或小于等于-2，即树失去平衡。虽然多个节点会失去平衡，但只需平衡最底部失去平衡的节点，树就会恢复平衡。

3. 旋转

让二叉搜索树恢复平衡的过程，称为旋转（Rorations）。旋转有两大基础操作：左旋和右旋。共有四种失去平衡类型：LL型、RR型、LR型、RL型。

3.1 RR 型

所谓的 RR 型就是节点的右子树的右子树导致其失去平衡，这时候需要左旋来解决。

对 25 左旋前后对比如下：

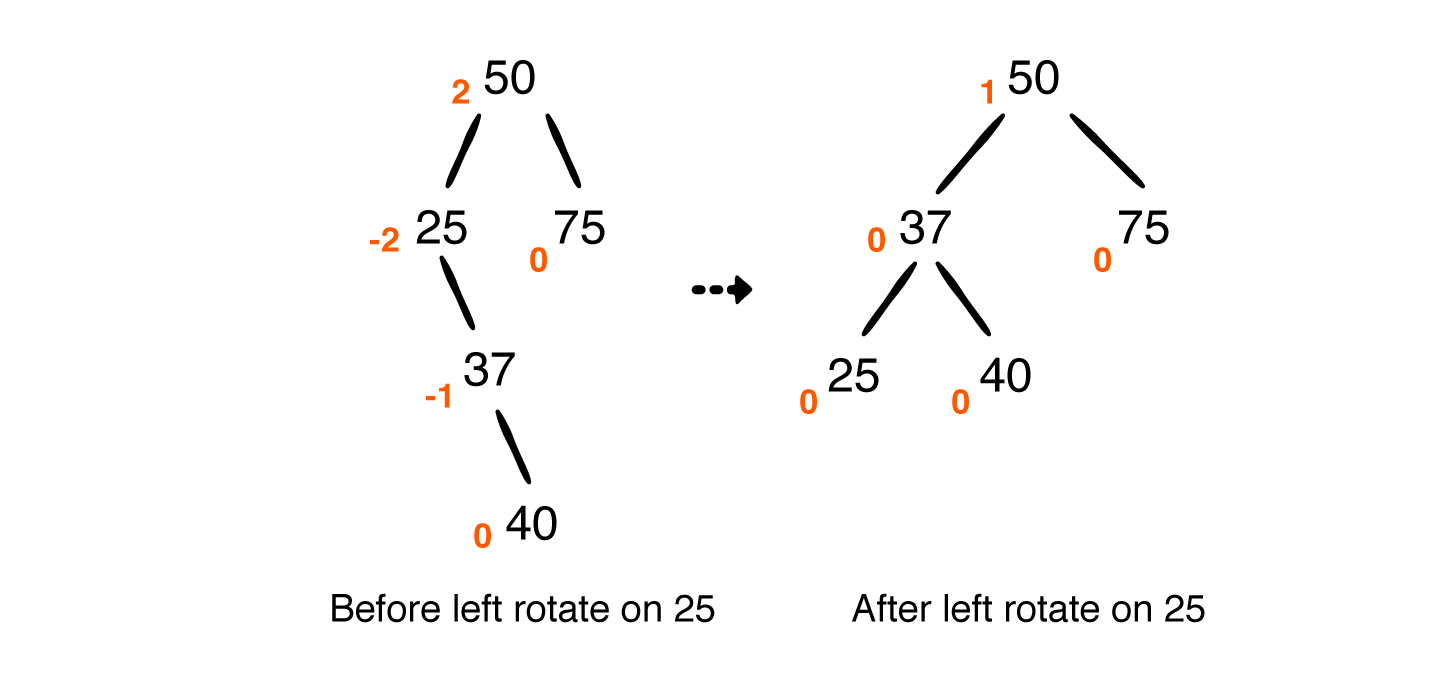
3.2 LL 型

所谓的 LL 型就是节点的左子树的左子树导致其失去平衡，这时候需要右旋来解决。

LL 型与 RR 型相反，当一系列左子树导致失衡，需进行右旋。

如下图中的 Z 导致其失去平衡，对 X 进行右旋操作如下：

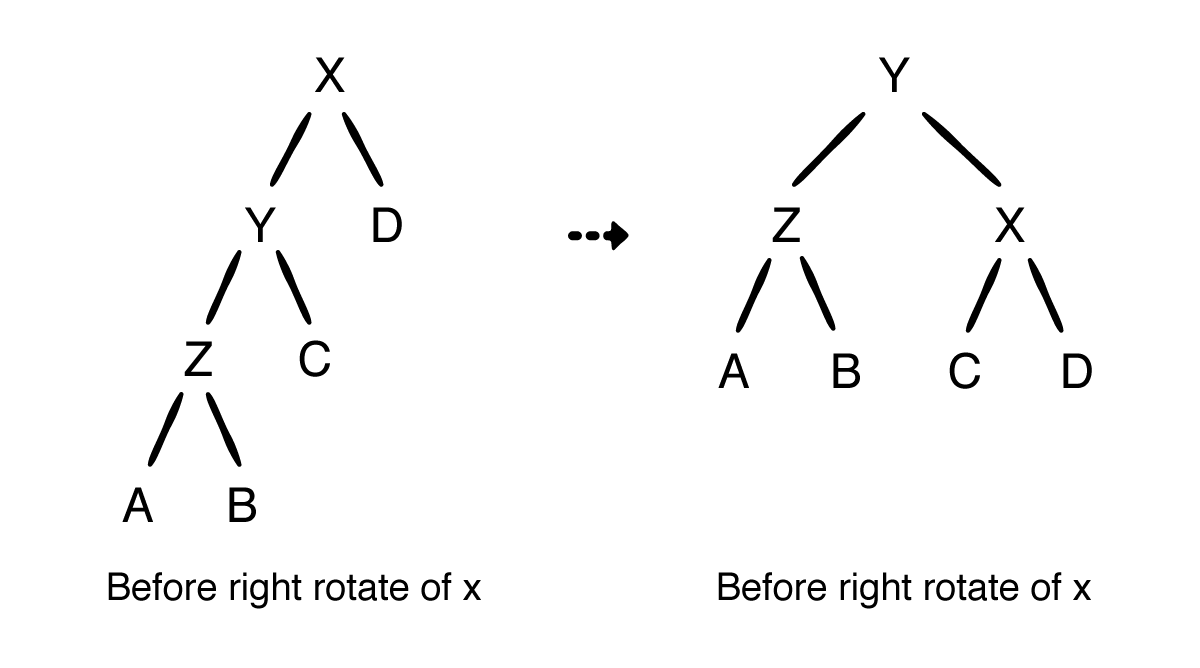
3.3 RL 型

RL 就是将节点插入到了右子树的左子树上，导致失去平衡。

前面遇到的都是子树在同一侧（左侧或右侧），当向其插入36时，将出现以下情况：

此时，左旋无法恢复平衡。需先对右子树右旋，再进行左旋。如下所示：

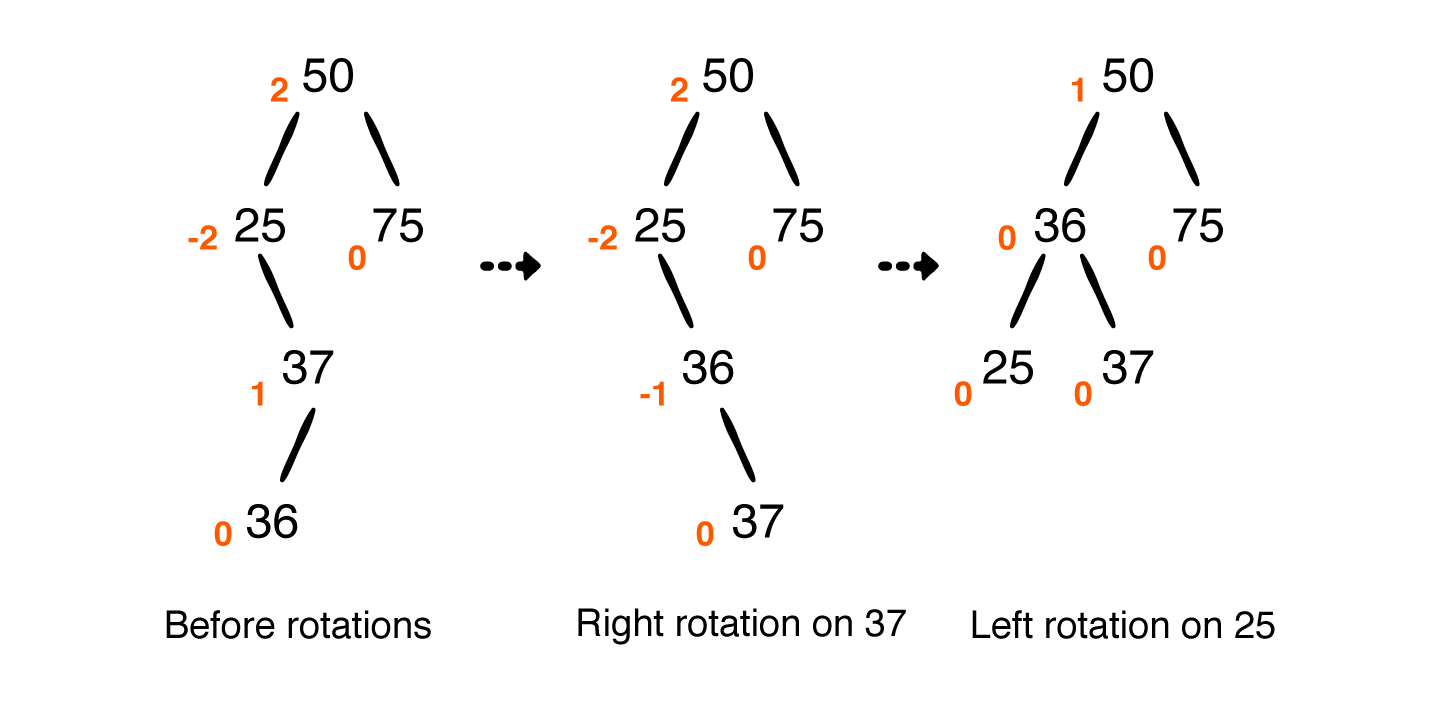
3.4 LR 型

LR 型和RL型刚好相反，如下所示：