参考文档：
最长回文子串
解题思路2：Manacher算法

1. 介绍

Manacher(又称"马拉车")算法通过对字符串预处理的方式求出最长回文子串， 算法时间复杂度为 O(n)

第一步: 添加分隔符

马拉车算法开始计算前在字符串中插入分隔符 #, 把奇数长度和偶数长度的字符串全部整合为一种情况，如下:
比如：

• 奇数长度：bbbabbc =====> #b#b#b#a#b#b#c#
• 偶数长度：cbbabb =====> #c#b#b#a#b#b#

加上分隔符后，我们对于每个点，只需去求回文串长度为奇数的情况，最后肯定包含我们所需要的结果，不需要再管偶数的情况。

第二步: 建立 p 数组，得到任意字符串回文半径长度

计算回文半径：以当前点为中心，最小半径为 1，然后同时往左右进行中心扩展，直至不能扩展为止。

建立 p 数组的意义在于得到任意字符串回文半径长度，因为每一个字符串本身都个可以看作是一个回文字符，而较前位置的回文字符半径会被较后位置的回文字符复用 (由于回文字符性质，前半部分存在的回文字符在后半部分同样存在)，因此复用半径可以直接减少 while 循环次数，直接降低时间复杂度。

以 cbbabb 为例，先画出下面的表格

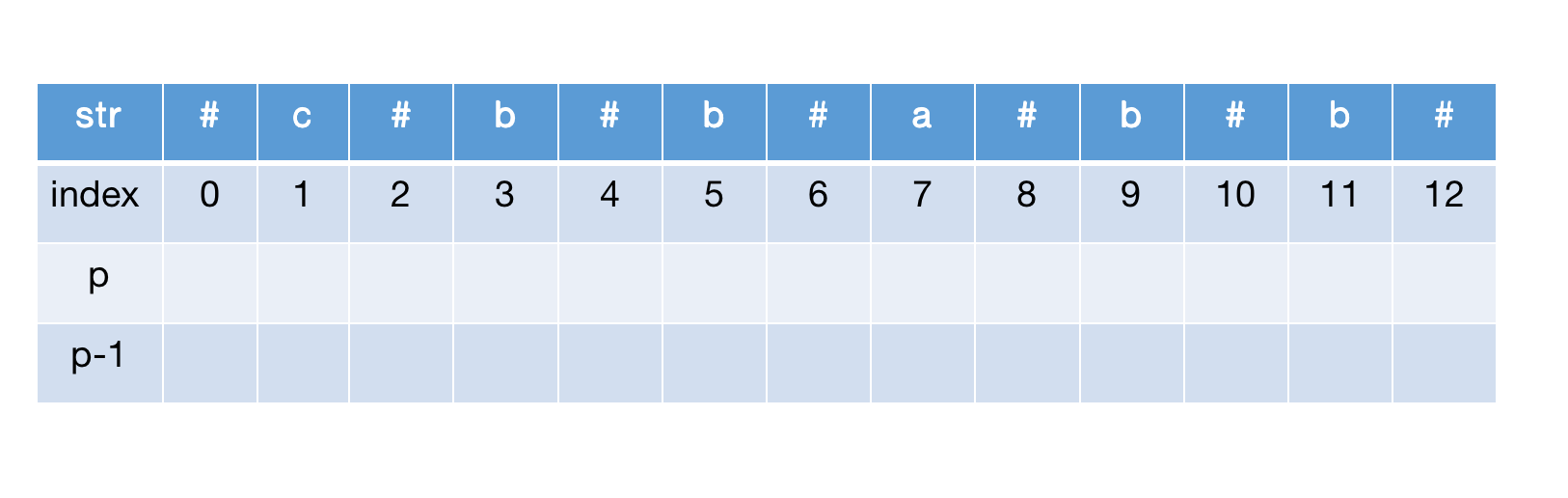
首先计算 str[0]，初始半径为 1，然后进行中心扩展，结果都到了边界，因此 str[0] 半径为1

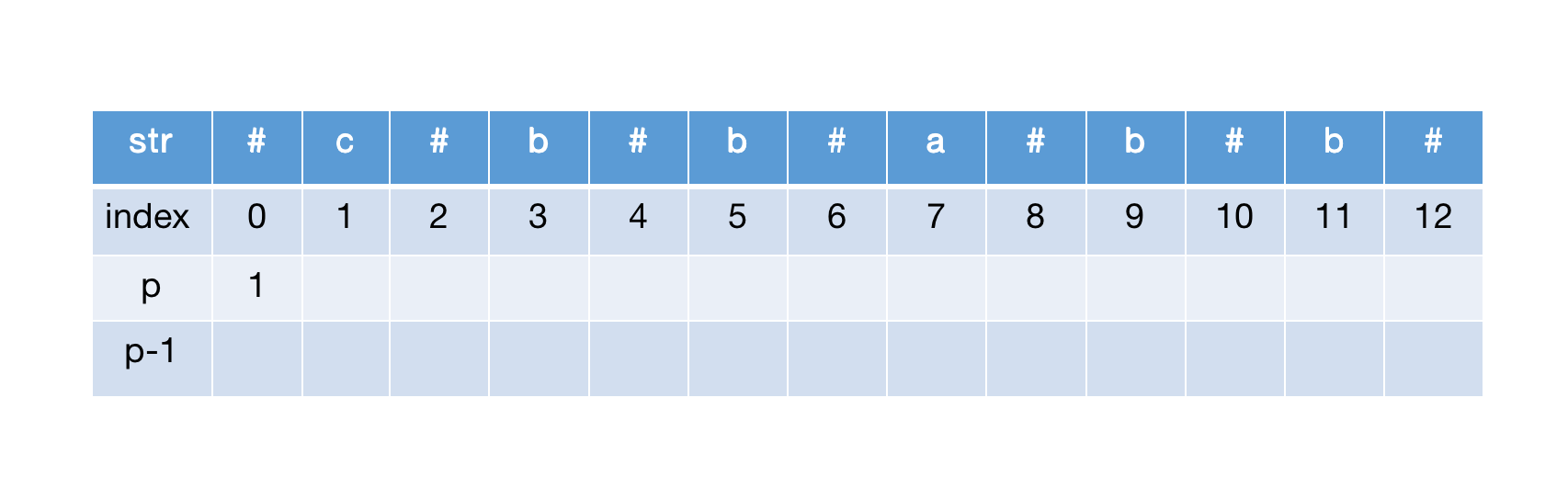
计算str[1]，同样初始化半径后中心扩展，str[0]=str[2]，半径加1，继续扩展到达边界

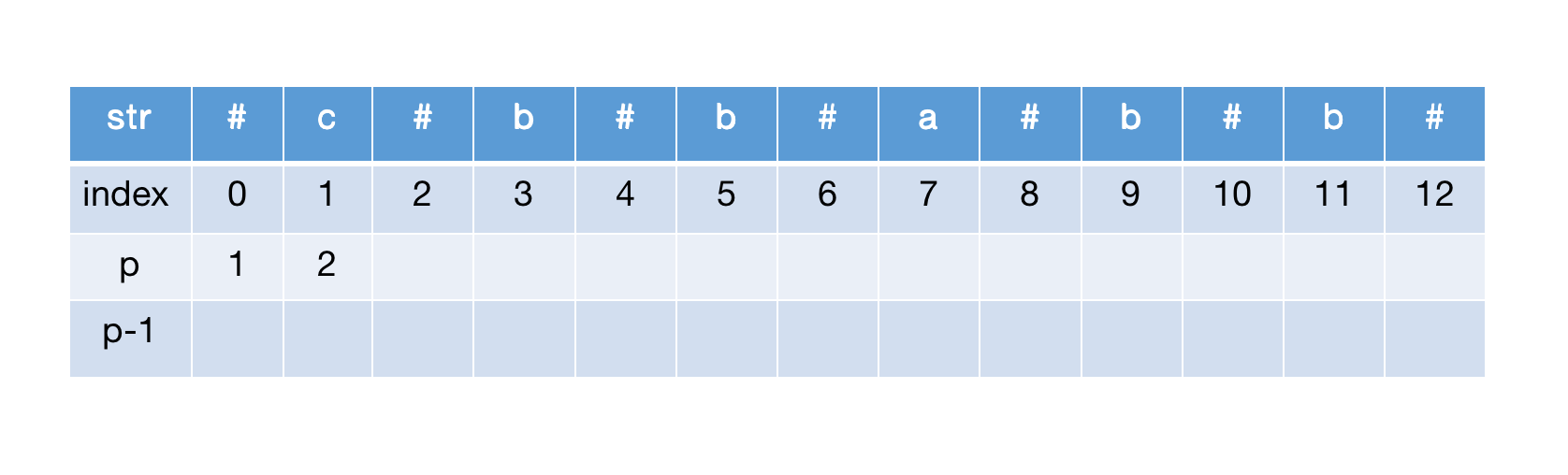
计算str[2]，左右扩展后到达边界

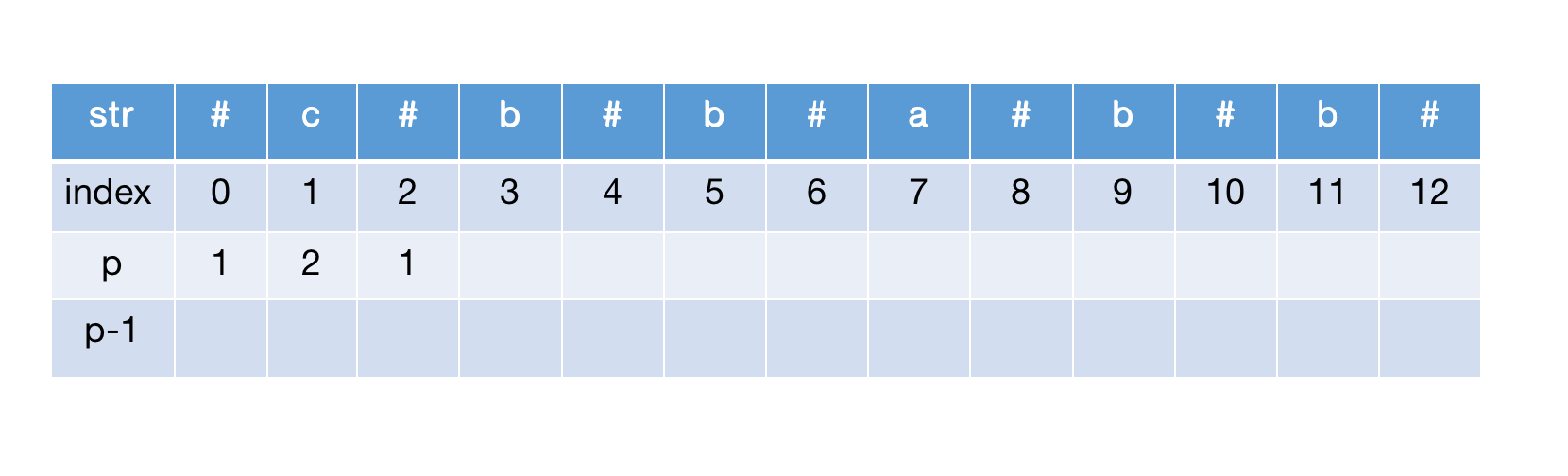
计算str[3]，左右扩展匹配，半径加1，继续扩展到达边界

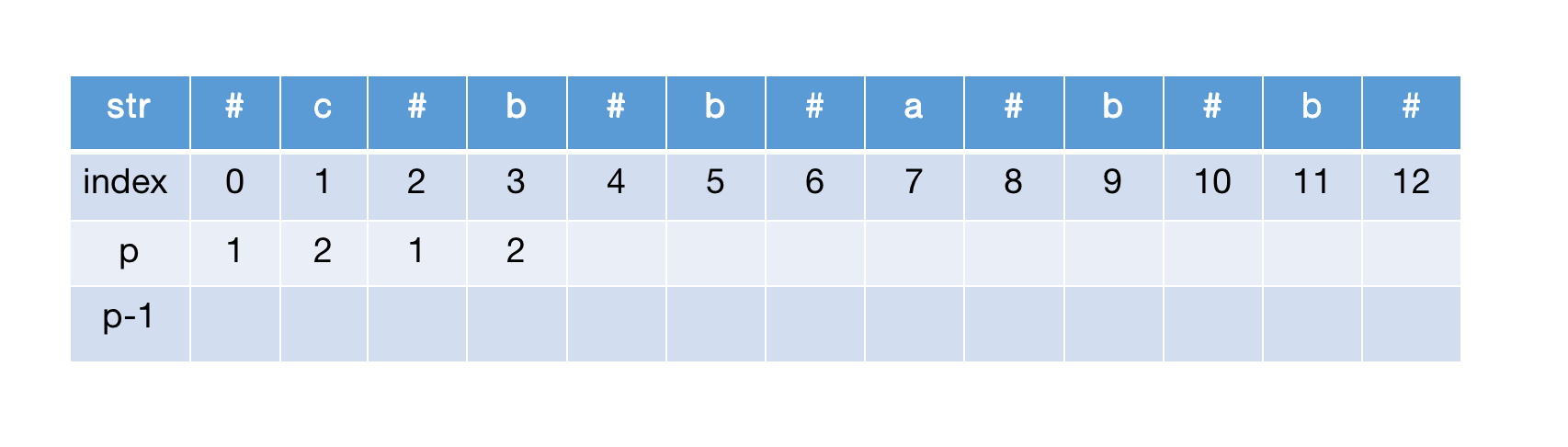
计算str[4]，左右扩展匹配，半径加1，继续扩展匹配，加1，继续扩展到达边界

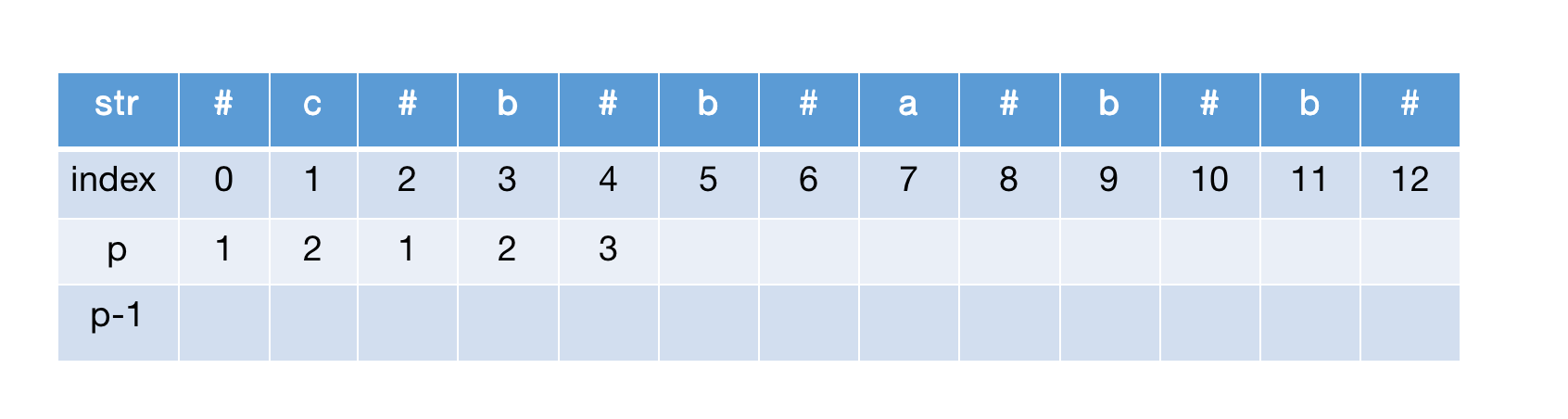
最终计算完的 p 数组:

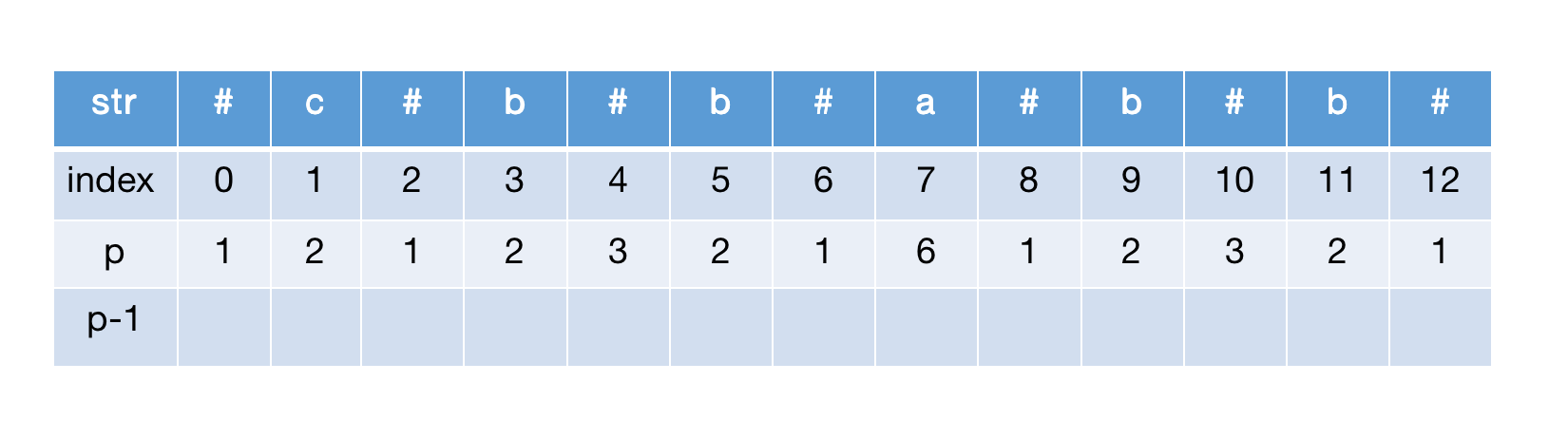
计算 p-1数组

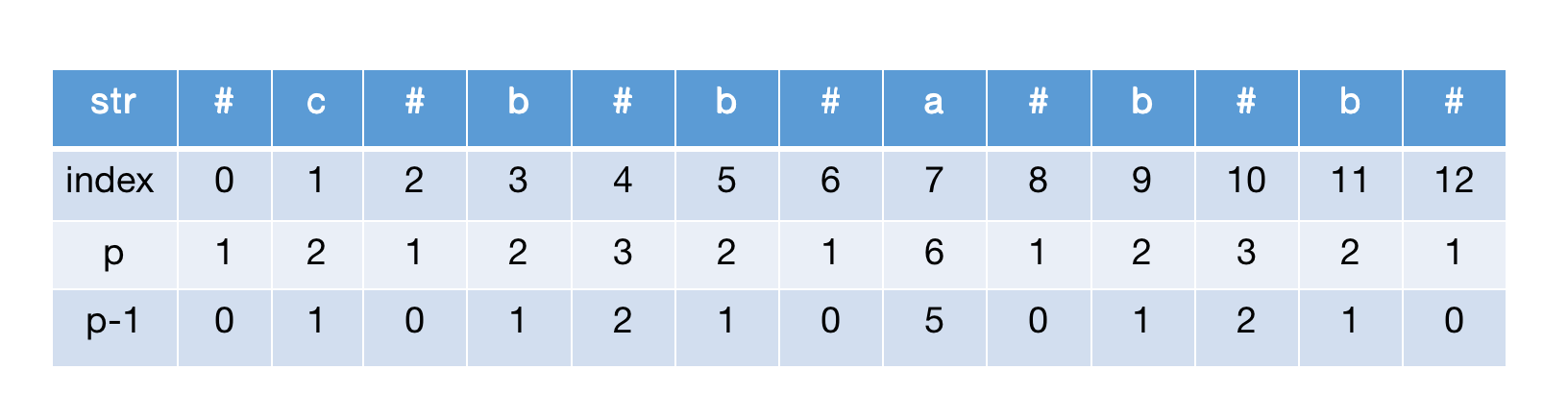
为什么还要 p-1 数组呢，这里简单分析下:

1. 已知长度为 n 的回文串添加分隔符后长度为 2n+1
2. 假设上面计算的中心半径为 p，那么容易得出 2p-1 = 2n+1
3. 可以算出 p = n+1 ===> p-1 = n, 因此得到 p-1数组即为当前点对应的回文子串的长度

第3步：如何在代码中计算 p 数组

以下图片为了方便理解把#符都省略掉

在第 2 步里介绍了马拉车算法核心在于复用回文串长度，在了解如何复用前先看下图:

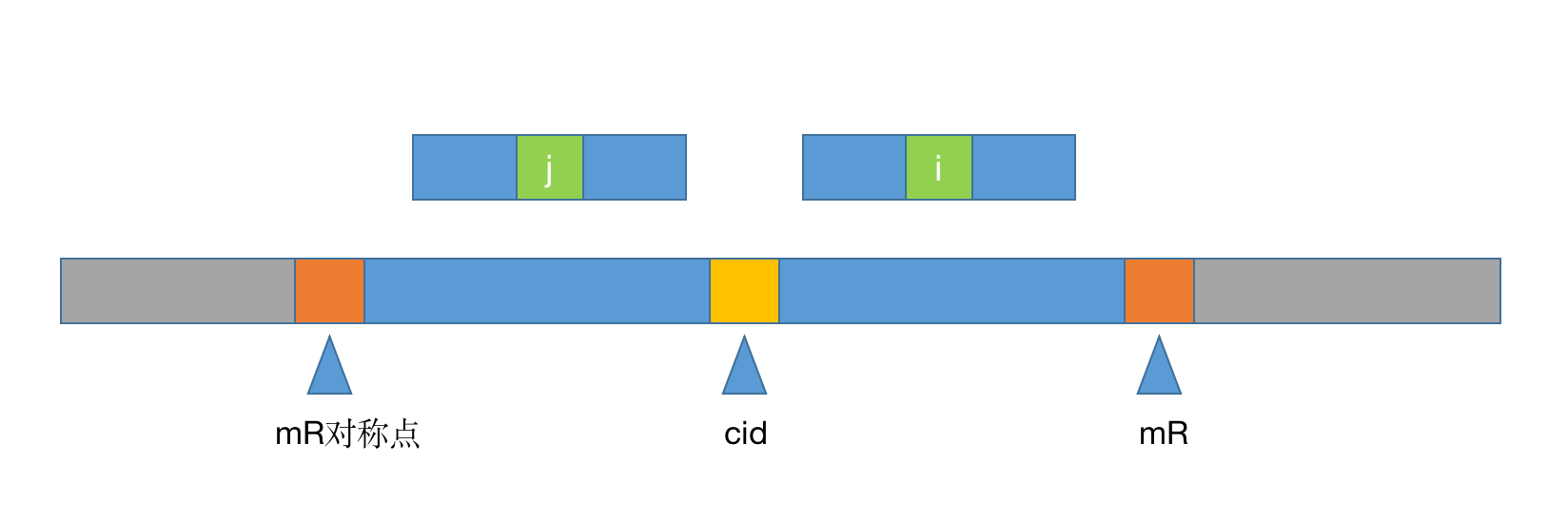
我们先介绍一下几个点的概念:

• mR 当前已知的所有点中，回文半径能达到的最远距离(点)。

• cid 为 MR 所对应的中心点。

从上图容易获得几个关键信息:

• i 和 j 是关于 cid 中心对称的，容易得出 j=2*cid - id 的性质
• mR 为最长回文串的最右边界，那么容易得出 cid+p[cid]-1 = mR
• cid 的左侧和右侧是相同的，那么 i 就可以复用 j 在 cid 长度区域内的部分
• 假设以 i 为中心的字符串也是回文串且最右侧不超过 mR，那么根据上图可以得出 i+p[i]-1<=mR

通过以上几个性质，先去计算最简单的一种情况:

• 假如 i<mR ，那么就可以考虑复用原则:

  • 如果以 j 的最左侧不超过 cid 的最左侧, 那么p[i]=p[2*cid-j]是成立的，如下图：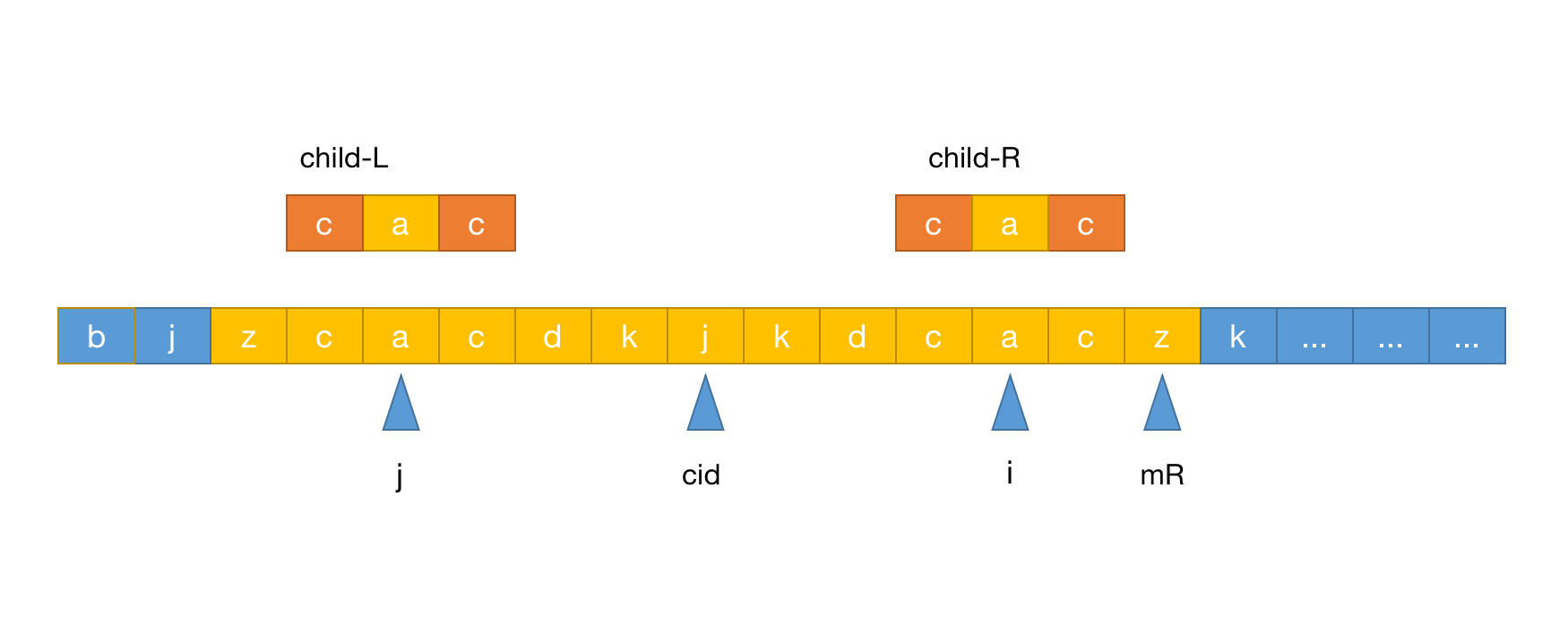
  • 假如以 j 为中心的回文串长度超过左边界，大概情况如下图:
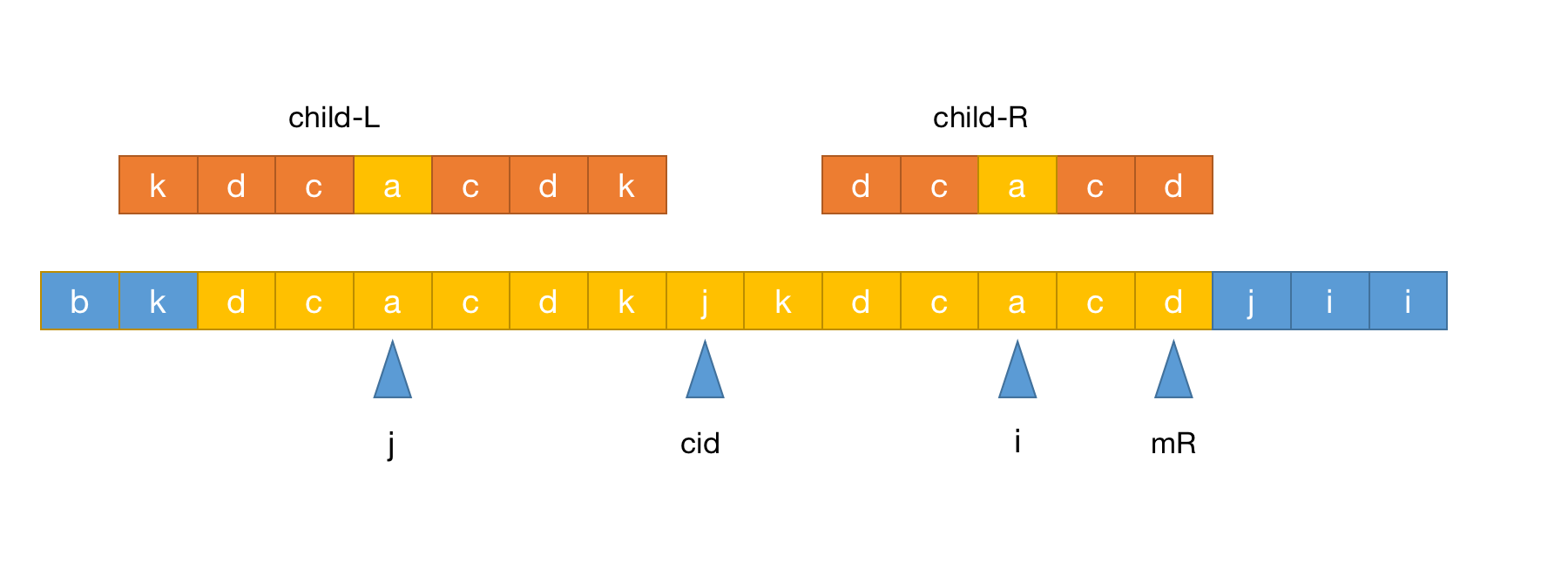
  • 从上图可以看出 j 的半径明显要比 i 要大，因此 p[i]=p[2*cid-j] 明显不成立，但是由于 j 半径已经越过左边界，根据对称原则 i 的右边界可以到达右边界 mR，也就是说可以得出 p[i]=mR-i+1，然后再对 i 点进行扩展，对超出的部分进行判断，即可求出 i 的回文半径。

• 假如 i>mR，这就简单了，赋值当前半径为 1，继续使用中心扩展去左右扩展匹配

  • 根据以上两点，总结出以下代码: p[i] = i < mR ? Math.min(p[2 * cId - i], mR - i + 1) : 1;
  • 当计算完 p[i] 后就要判断当前 i 的半径是否超过 mR，超过则更新 mR 和 cid

2. 代码实现

import java.util.ArrayList;

class Solution {

    public String longestPalindrome(String s) {
        // 标记最长回文子串的开始点和结束点
        int start = 0, end = -1;
        s = wrapperStr(s);
        ArrayList<Integer> list = new ArrayList<>();
        // 初始化 right 和 cid
        int right = -1, cid = -1;
        for (int i = 0; i < s.length(); i++) {
            int currentArmLen;
            if (i <= right) {
                // 复用对称点的信息
                int armLen = Math.min(list.get(2 * cid - i), right - i + 1);
                // 扩展
                currentArmLen = expand(s, i - armLen, i + armLen);
            } else {
                // 扩展
                currentArmLen = expand(s, i, i);
            }
            // 记录当前点
            list.add(currentArmLen);

            // 更新 cid 和 right
            if (i + currentArmLen > right) {
                cid = i;
                right = i + currentArmLen - 1;
            }

            // 标记答案
            if (currentArmLen * 2 - 1 > end - start) {
                start = i - currentArmLen + 1;
                end = i + currentArmLen - 1;
            }
        }

        return getAns(s, start, end);

    }

    // 预处理字符串
    private String wrapperStr(String s) {
        StringBuilder sb = new StringBuilder("#");
        for (int i = 0; i < s.length(); i++) {
            sb.append(s.charAt(i));
            sb.append("#");
        }
        return sb.toString();
    }

    // 字符串向两边扩展，返回当前点的回文半径
    public int expand(String s, int left, int right) {
        while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
            left--;
            right++;
        }
        return (right - left) / 2;
    }

    private String getAns(String s, int start, int end) {
        StringBuilder ans = new StringBuilder();
        for (int i = start; i <= end; ++i) {
            if (s.charAt(i) != '#') {
                ans.append(s.charAt(i));
            }
        }
        return ans.toString();
    }
}