参考文档:
漫画:什么是B-树?
漫画:什么是B+树?
1. B- 树
B- 树念 B 树,不念 B 减树
1.1 数据库索引为什么不使用二叉查找树?
其实从算法逻辑上来讲,二叉查找树查找速度和比较次数都是最小的。但是,我们不得不考虑一个现实问题:磁盘 IO。
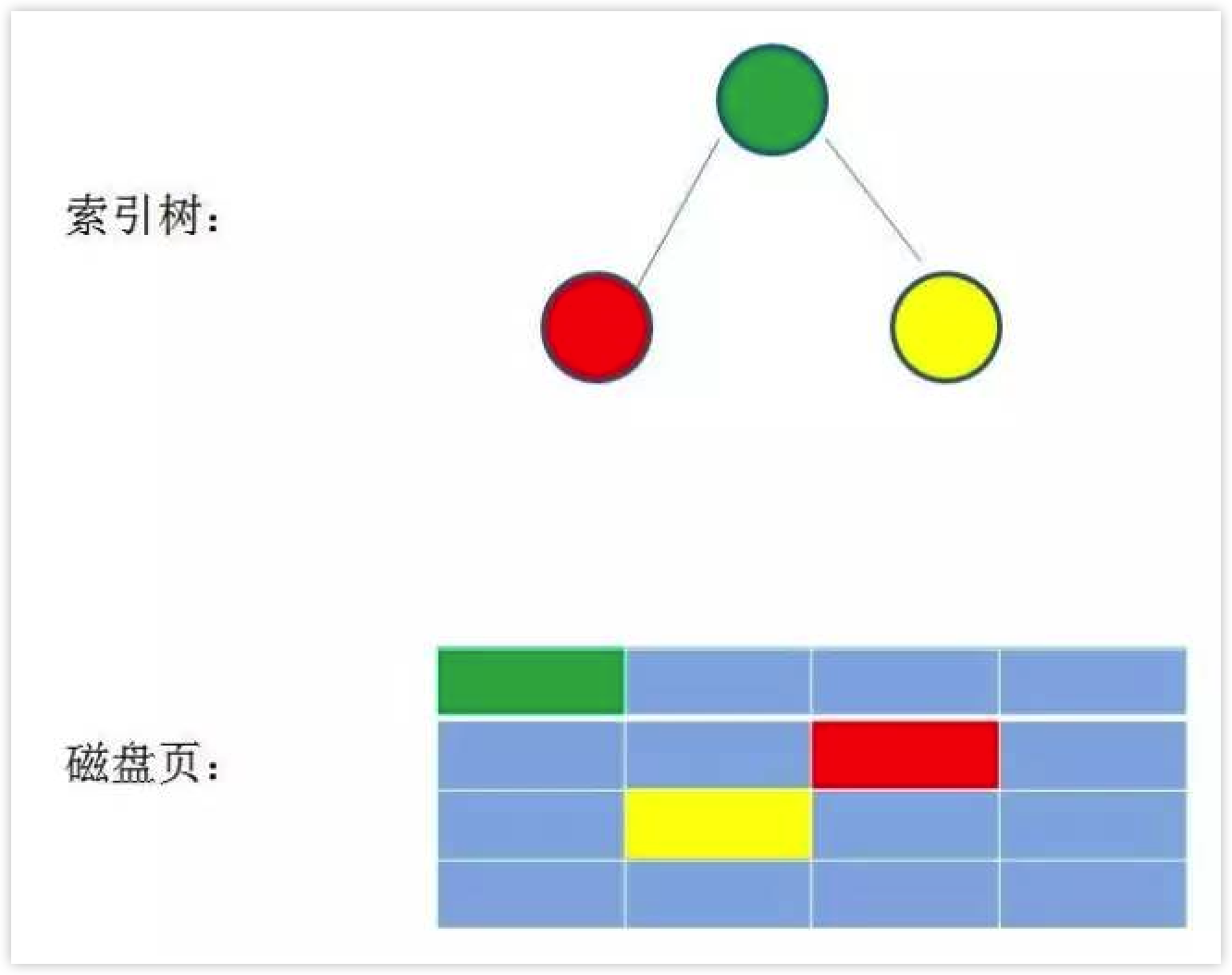
数据库索引是存储在磁盘上的,当数据量比较大的时候,索引的大小可能有几个G甚至更多。
当我们利用索引查询的时候,能把整个索引全部加载到内存吗?显然不可能。能做的只有逐一加载每一个磁盘页,这里的磁盘页对应着索引树的节点。
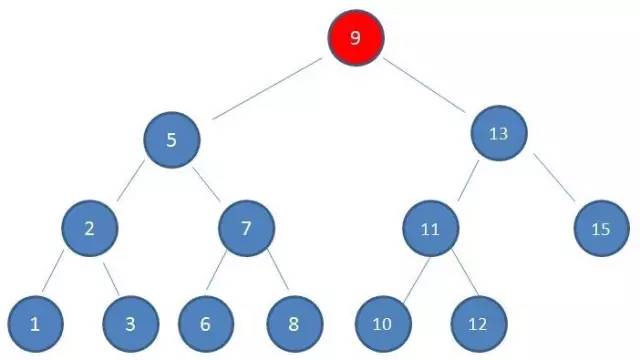
如果我们利用二叉查找树作为索引结构,情形是什么样呢?假设树的高度是 4,查找的值是10,那么流程如下:
二叉查找树的结构:

第1次磁盘IO:
第2次磁盘IO:

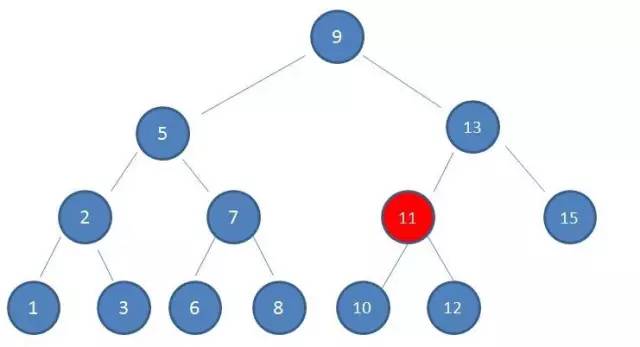
第3次磁盘IO:
第4次磁盘IO:
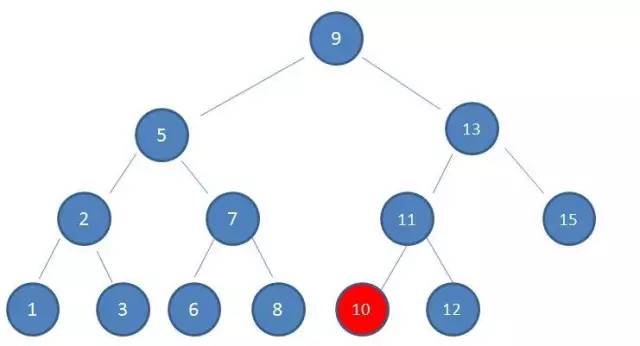
可见,磁盘 IO 次数由树的高度决定
1.2 B- 树
为了减少磁盘 IO 次数,我们就需要把原本 "瘦高"的树结构变得 "矮胖"。这就是 B- 树的特征之一。
B 树是一种多路平衡查找树,它的每一个节点最多包含 k 个孩子,k 被称为 B 树的阶。k 的大小取决于磁盘页的大小。
下面来具体介绍一下 B- 树(Balance Tree),一个 m 阶的 B 树具有如下几个特征:
- 根结点至少有两个子女。
- 每个中间节点都包含 k-1 个元素和 k 个孩子,其中 m/2 <= k <= m
- 每一个叶子节点都包含 k-1个元素,其中 m/2 <= k <= m
- 所有的叶子结点都位于同一层。
- 每个节点中的元素从小到大排列,节点当中 k-1 个元素正好是 k 个孩子包含的元素的值域分划。
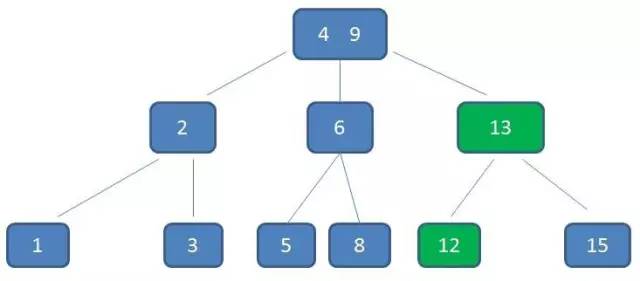
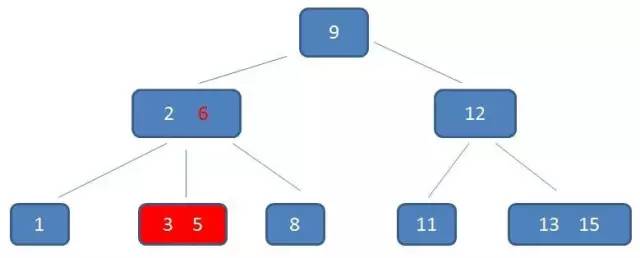
我们以一个 3 阶 B- 树为例,来看看 B- 树的具体结构。树中的具体元素和刚才的二叉查找树是一样的。
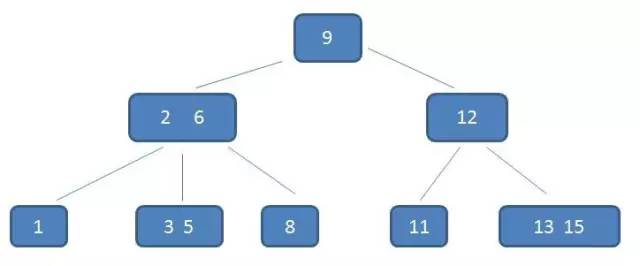
这棵树中,咱们重点来看(2,6) 节点。该节点有两个元素2和6,又有三个孩子1,(3,5),8。
其中1小于元素2,(3,5)在元素 2,6之间,8大于-(3,5),正好符合刚刚所列的几条特征。
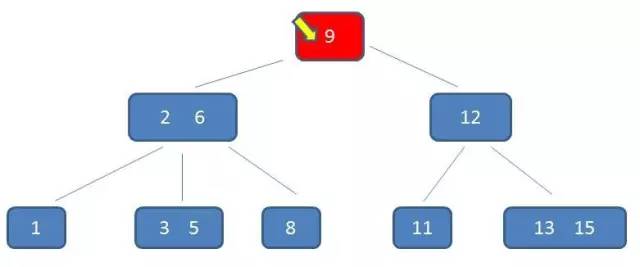
假如我们要查询 5。
第 1 次磁盘 IO:

在内存中定位(和9比较):
第 2 次磁盘 IO:
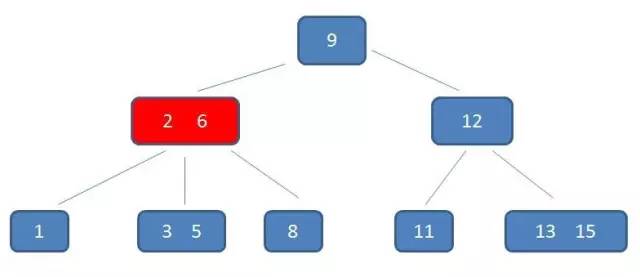
在内存中定位(和2,6比较):
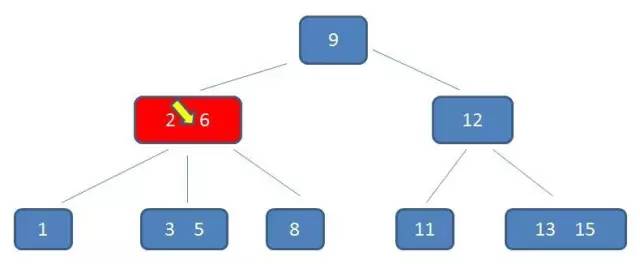
第3次磁盘IO:

在内存中定位(和3,5比较):
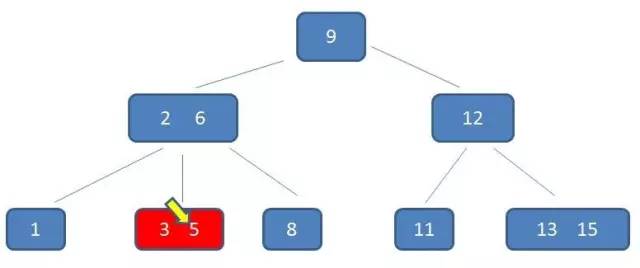
通过整个流程我们可以看出,B-树在查询中的比较次数其实不比二叉查找树少,尤其当单一节点中的元素数量很多时。
可是相比磁盘 IO 的速度,内存中的比较耗时几乎可以忽略。所以只要树的高度足够低,IO 次数足够少,就可以提升查找性能。
相比之下节点内部元素多一些也没有关系,仅仅是多了几次内存交互,只要不超过磁盘页的大小即可。这就是 B- 树的优势之一。
1.3 插入节点
我们举一个最典型的例子,假设我们要插入 4。
自顶向下查找4的节点位置,发现4应当插入到节点元素3,5之间。
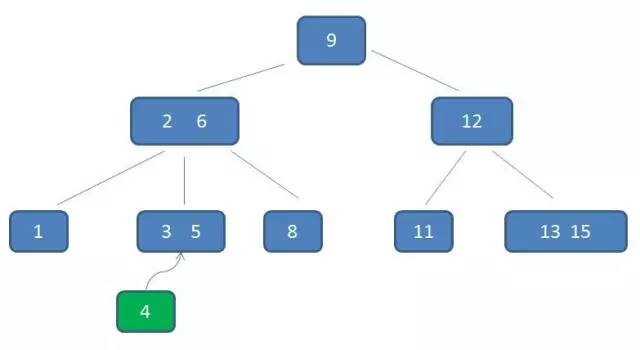
节点3,5已经是两元素节点,无法再增加。父亲节点 2, 6 也是两元素节点,也无法再增加。根节点9是单元素节点,可以升级为两元素节点。于是拆分节点3,5与节点2,6,让根节点9升级为两元素节点4,9。节点6独立为根节点的第二个孩子。
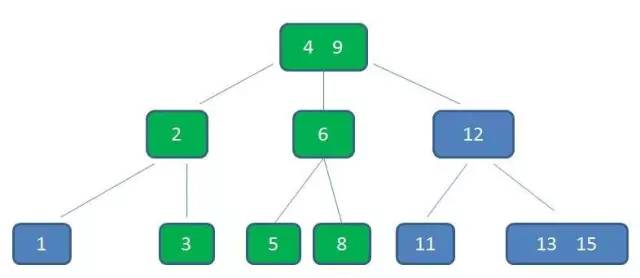
由此可见,B- 树始终维持多路平衡,这也是 B- 树的一大优势:自平衡。
1.4 删除节点
假设我们要删除 11。
自顶向下查找元素11的节点位置。
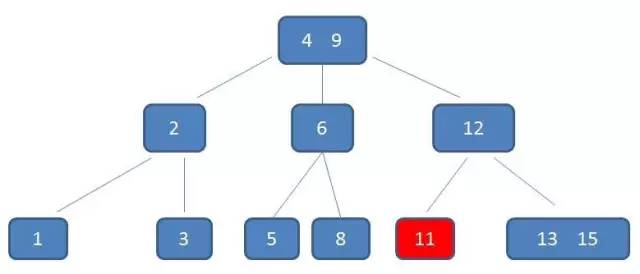
删除11后,节点12只有一个孩子,不符合B树规范。因此找出12,13,15三个节点的中位数13,取代节点12,而节点12自身下移成为第一个孩子。(这个过程称为左旋)

B- 树主要应用于文件系统以及部分数据库索引,比如著名的非关系型数据库 MongoDB。
而大部分关系型数据库,比如 Mysql,则使用 B+ 树作为索引。
2. B+ 树
2.1 B+ 树
B+ 树是基于B-树的一种变体,有着比B-树更高的查询性能。
B+ 树和 B- 树有一些共同点,但是B+ 树也具备一些新的特征。
- 有 k 个子树的中间节点包含有 k 个元素(B树中是k-1个元素),每个元素不保存数据,只用来索引,所有数据都保存在叶子节点。
- 所有的叶子结点中包含了全部元素的信息,及指向含这些元素记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接。
- 所有的中间节点元素都同时存在于子节点,在子节点元素中是最大(或最小)元素。
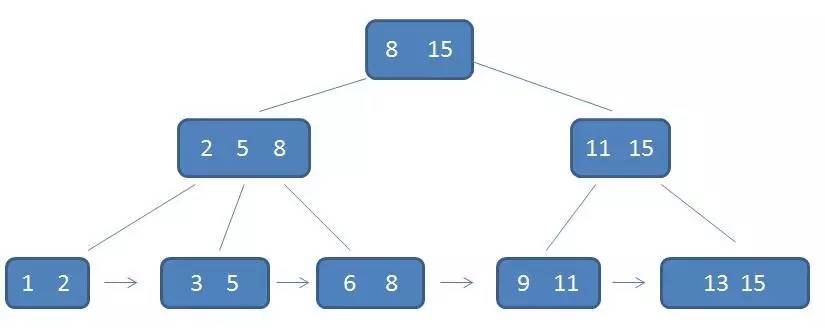
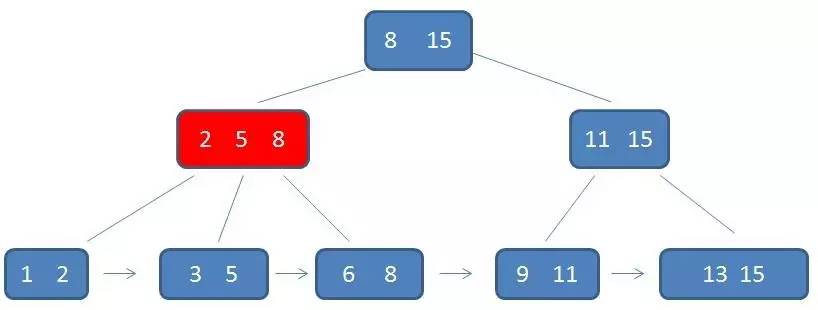
可见,叶子节点都用指针连在一起,父节点都出现在子节点中,且是子节点的最大(或最小)元素。

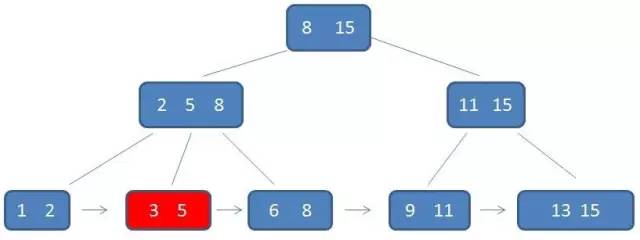
在上面这棵树中,根节点元素8是子节点2,5,8 的最大元素,也是叶子节点6,8 的最大元素。
根节点元素15 是子节点 11,15的最大元素,也是叶子节点13,15 的最大元素。
需要注意的是,根节点的最大元素(这里是15),也就等同于整个 B+ 树的最大元素。以后无论插入删除多少元素,始终要保持最大元素在根节点当中。
至于叶子节点,由于父节点的元素都出现在子节点,因此所有叶子节点包含了全量元素信息。
并且每一个叶子节点都带有指向下一个节点的指针,形成了一个有序链表。

2.2 卫星数据
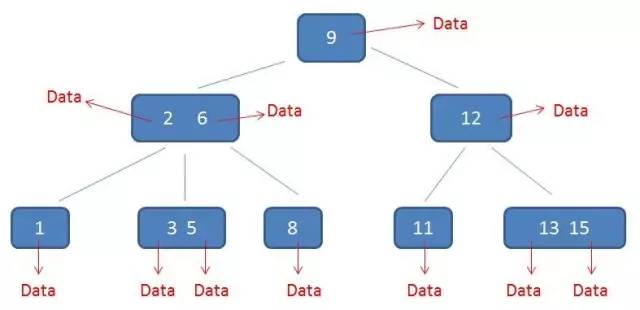
所谓卫星数据,指的是索引元素所指向的数据记录,比如数据库中的某一行。在B-树中,无论中间节点还是叶子节点都带有卫星数据。
B-树中的卫星数据(Satellite Information):
而在B+ 树当中,只有叶子节点带有卫星数据,其余中间节点仅仅是索引,没有任何数据关联。

在数据库的聚集索引(Clustered Index)中,叶子节点直接包含卫星数据。在非聚集索引(NonClustered Index)中,叶子节点带有指向卫星数据的指针。
2.3 B+ 树的优点
B+ 树的好处主要体现在查询性能上。下面我们分别通过单行查询和范围查询来做分析。
2.3.1 单元素查询
在单元素查询的时候,B+树会自顶向下逐层查找节点,最终找到匹配的叶子节点。比如我们要查找的是元素3
第一次磁盘 IO:

第二次磁盘IO:
第三次磁盘IO:
- B+ 树的中间节点没有卫星数据,所以同样大小的磁盘页可以容纳更多的节点元素。
- 这就意味着,数据量相同的情况下,B+ 树的结构比 B-树更加矮胖,因此查询时IO 次数也更少,
- B+ 树的查询必须最终查找到叶子节点,而B-树只要找到匹配元素即可,无论匹配元素处于中间节点还是叶子节点。因此,B-树的查找性能并不稳定(最好情况是只查根节点,最坏情况是查到叶子节点)。而B+树的每一次查找都是稳定的。
2.3.2 范围查询
下面我们再来看看范围查询。B-树如何做范围查询呢?只能依靠繁琐的中序遍历。比如我们要查询范围为3到 11的元素:
B-树的范围查找过程
自顶向下,查找到范围的下限(3):

中序遍历到元素6:
中序遍历到元素8:

中序遍历到元素9:

中序遍历到元素11,遍历结束:

B+树的范围查找过程
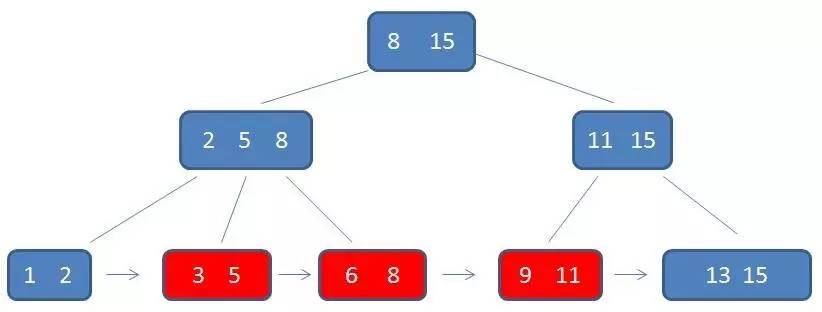
自顶向下,查找到范围的下限(3):

通过链表指针,遍历到元素6, 8:

通过链表指针,遍历到元素9, 11,遍历结束:
综合起来,B+ 树相比B-树的优势有三个:
- IO 次数更少
- 查询性能稳定
- 范围查询简便。
总结
B+ 树优点有如下几点:
- 单一节点存储更多的元素,使得查询的 IO 次数更少。
- 所有查询都要查找到叶子节点,查询性能稳定。
- 所有叶子节点形成有序链表,便于范围查询。
