参考文献:什么是差分数组?
背景
如果给你一个包含5000万个元素的数组,然后会有频繁区间修改操作,那什么是频繁的区间修改操作呢?比如让第1个数到第1000万个数每个数都加上1,而且这种操作时频繁的。
此时你应该怎么做?很容易想到的是,从第1个数开始遍历,一直遍历到第1000万个数,然后每个数都加上1,如果这种操作很频繁的话,那这种暴力的方法在一些实时的系统中可能就拉跨了。
因此,今天的主角就出现了——差分数组。
算法原型
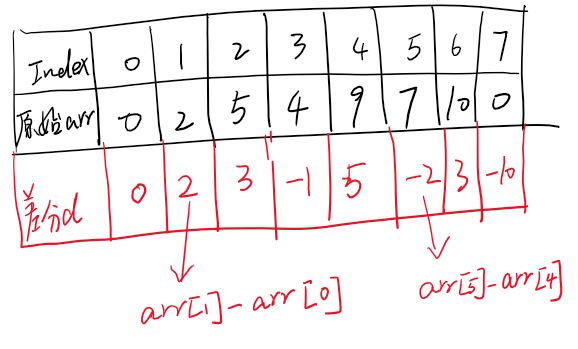
比如我们现在有一个数组arr,arr={0,2,5,4,9,7,10,0}

那么差分数组是什么呢?其实差分数组本质上也是一个数组,我们暂且定义差分数组为d,差分数组d的大小和原来arr数组大小一样,而且 d[i]=arr[i]-arr[i-1](i≠0),且d[i]=0,它的含义是什么?就是原来数组i位置上的元素和i-1位置上的元素作差,得到的值就是d[i]的值。
所以,例子中的arr数组其对应的差分数组值如下图所示。
那么构造了这么个玩意有什么用呢?难道是来浪费宝贵的内存空间的?嗯,确实是来浪费宝贵的内存了,但是却换了时间上的高效。
现在我们有这么一个区间修改操作,即在区间1~4上,所有的数值都加上3.
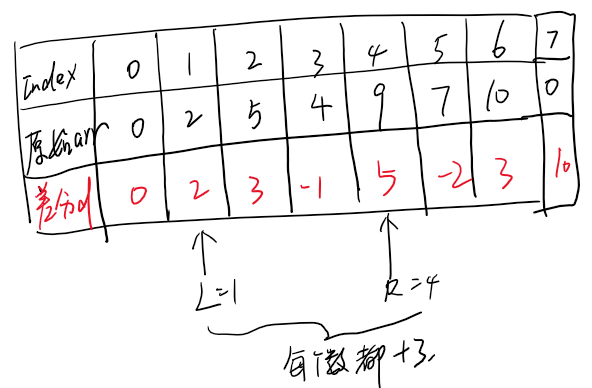
我们不要傻傻地遍历arr数组的[1,4]范围,然后再分别给每个值加上3,我们此时更改差分数组d即可。
显而易见,差分数组d在[2,4]范围内的值都不用改变,只需要改变差分数组位置1和位置5的值即可,即d[1]=d[1]+3,而d[5]=d[5]-3,其余不变,为什么呢?因为差分数组的定义——d[i]=arr[i]-arr[i-1]

现在,我们如何根据差分数组d来推测arr中某一个位置的值呢?
如,此时,我们想知道arr[1]的值,我们不能直接通过arr[1]得到原来的值,因为在区间修改的操作中我们并没有修改arr的值。
我们之间求差分数组的前缀和即可得到改动后的数组。
总结
可以看到,如果需要对 L-R 范围内所有数都进行相同的操作,我们不需要从 L-R 遍历 arr 然后在每个值上进行相同操作,只需要在差分数组 d 中改变 L 和 R+1的值即可。但是在查询 arr 数组中某个位置的数时,却要根据差分数组从前往后递推求值。
所以,该方法适用于区间频繁修改,而且这个区间范围是比较大的,离线查询的情况。
