归并排序

参考链接：
图解排序算法(四)之归并排序

  归并排序是利用归并的思想实现的排序方法，该算法采用经典的分治策略【分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"整合"在一起，即分而治之】。

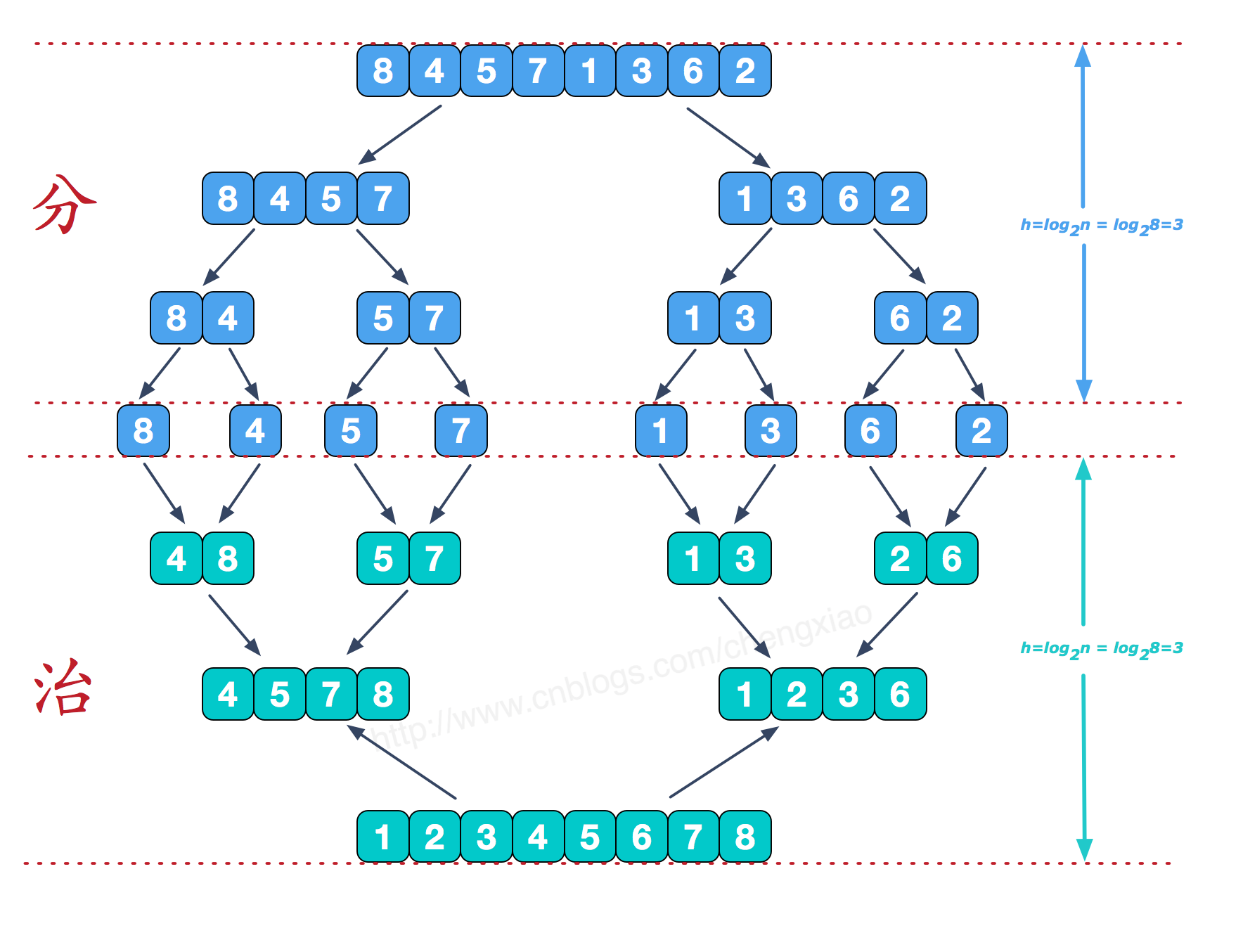
  根据图所示，首先将序列递归分解，直到分成的都是一个数，然后递归返回，数组中的小单元开始进行合并，在合并的时候进行排序，每个合成的序列都为有序序列。接下来，我们来看最后一次合并。

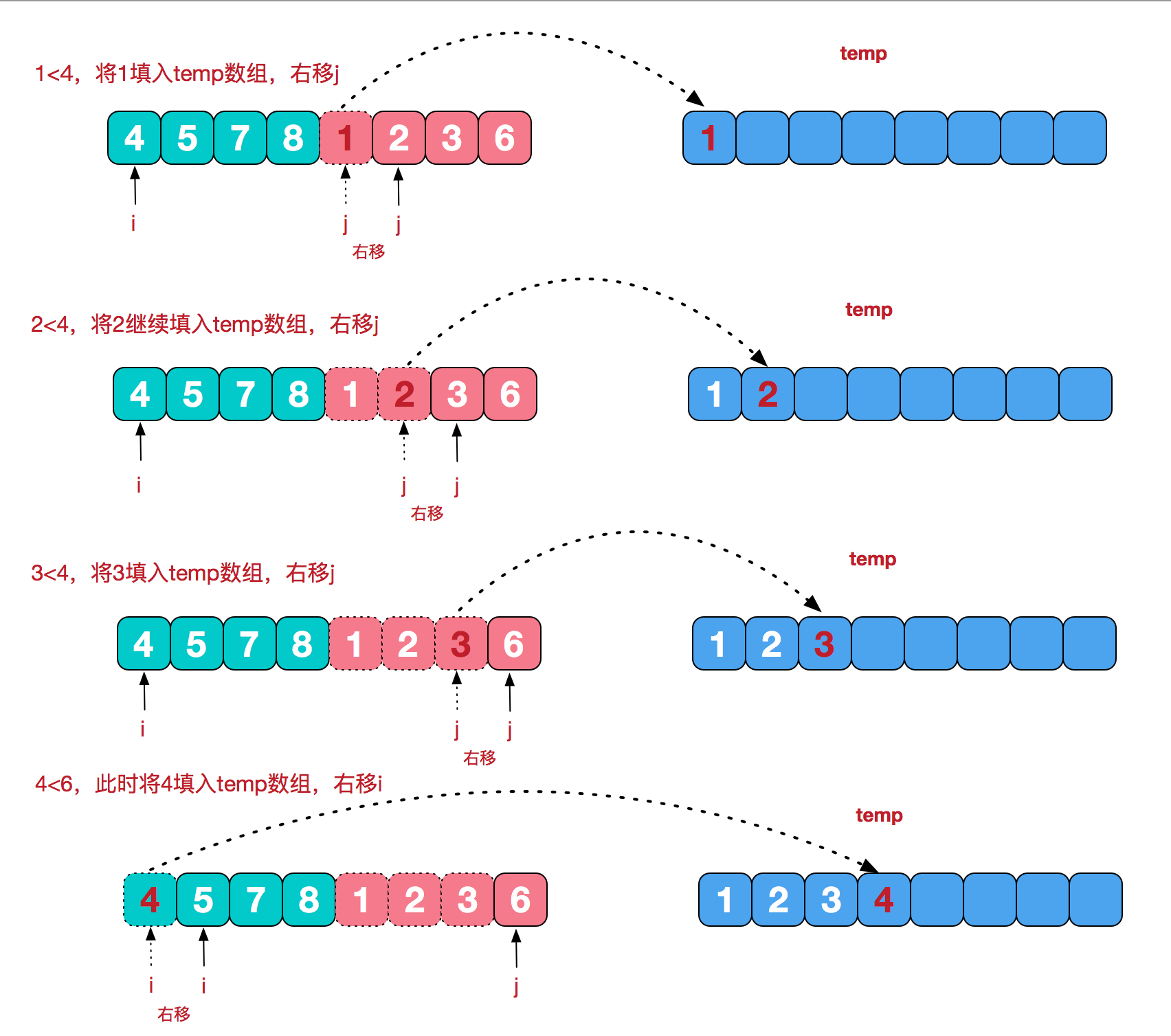
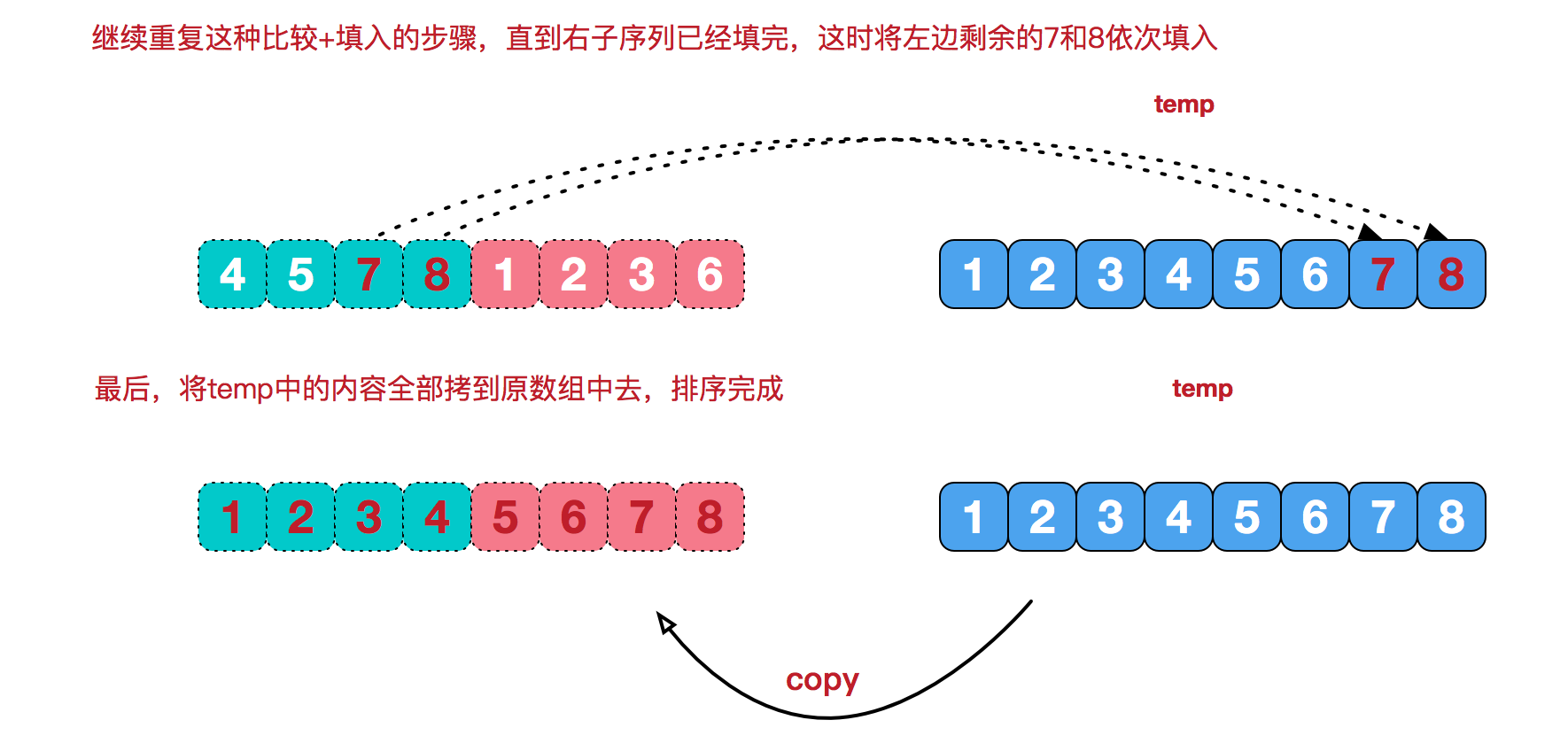
代码实现中，先将原数组数据复制进了temp数组，然后将合并形成的序列填进了原数组，Java实现：

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.List;

public class MergeSort {
    //算法类不允许产生任何实例
    private MergeSort() {
    }

    //将arr[l...mid] 和arr[mid+1....r] 两部分进行归并
    private static <T extends Comparable<T>> void merge(T[] arr, int l, int mid, int r) {
        T[] temp = Arrays.copyOfRange(arr, l, r + 1);
        //初始化，i指向左半部分的起始；j指向右半部分，索引位置为mid+1
        int i = l, j = mid + 1;
        for (int k = l; k <= r; k++) {
            if (i > mid) {
                //左半部分元素已经全部处理完毕
                arr[k] = temp[j - l];
                j++;
            } else if (j > r) {
                //右半部分元素已经全部处理完毕
                arr[k] = temp[i - l];
                i++;
            } else if (temp[i - l].compareTo(temp[j - l]) <= 0) {
                //左半部分所指元素<右半部分所指元素
                arr[k] = temp[i - l];
                i++;
            } else {
                arr[k] = temp[j - l];
                j++;
            }
        }
    }

    //递归进行排序
    private static <T extends Comparable<T>> void sort(T[] arr, int l, int r) {
        if (l >= r)
            return;
        int mid = (r + l) / 2;
        sort(arr, l, mid);
        sort(arr, mid + 1, r);
        merge(arr, l, mid, r);
    }

    //T需要实现Comparable接口，即T需为可排序的
    public static <T extends Comparable<T>> void mergeSort(T[] arr) {
        int n = arr.length;
        sort(arr, 0, n - 1);
    }

    public static void main(String[] args) {
        List<Integer> list = new ArrayList<>();
        Collections.addAll(list, 2, 5, 6, 1, 7, 9, 3, 0);
        //T[] toArray(T[] a):返回数组，返回数组的运行时类型与指定数组的运行时类型相同
        Integer[] nums = list.toArray(new Integer[0]);
        mergeSort(nums);
        for (Integer num : nums) {
            System.out.print(num + " ");
        }
    }
} 

归并排序是稳定的。
时间复杂度：
  每次合并操作的平均时间复杂度为O(n)，而完全二叉树的深度为log2n，总的平均时间复杂度为O(nlogn)。
空间复杂度：
  O(n)。