欧拉定理:

phi(n)为n的欧拉函数值,当n为质数时,n的欧拉函数值为n-1
降幂公式:
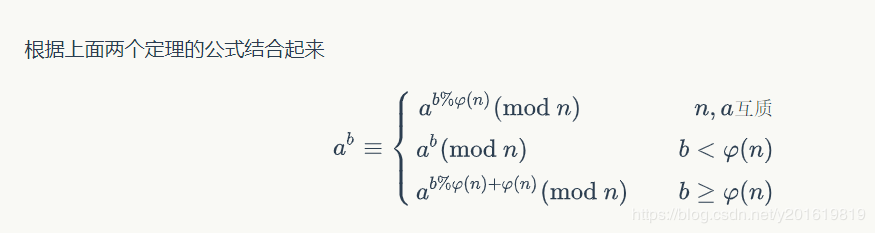
对于一个问题求 a^b %n
可以直接根据右边的条件把式子转换成上面三个中的一个
例题:
题目大意:求2n%1e9+7结果,1<=n<=10100000
题解:n很大,所以要用大数取模。p与2互质,所以2n%p==2(n%phi§)%p,又因为p为质数,所以phi§=p-1,
那么 2^n mod p= 2^(x*(p-1)+n%(p-1)) mod p = 2^(n%(p-1)) mod p
大数取模求出n%(p-1) 然后快速幂就行了。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
char s[2000005];
ll quick(ll a, ll b) {
ll res = 1;
while (b) {
if (b & 1) res = (res*a) % mod;
b >>= 1;
a = (a*a) % mod;
}
return res;
}
int main() {
scanf("%s", s);
ll n = s[0] - '0';
ll MOD = mod - 1;
int len = strlen(s);
for (int i = 1; i < len; i++) {
n = (n * 10 + s[i] - '0') % MOD;
}
ll N = quick(2, n);
printf("%lld\n", N);
}
